我们来继续学习 GLSL 的相关编程知识。 本节主要讲解 GLSL 中的运算。

GLSL 中的运算

注意 GLSL 中没有隐式转换，即便在多维向量中也没有，类似下面这样的的赋值都是错误的：

int a = 2.0;
vec4 v4=vec4(1.0, 1.0, 2, 1.0);

运算符

GLSL 中的运算符与 C 语言的大致相似，但由于存在 向量 和 矩阵 这两种基本类型，所以还是有一些不同的。见下表：

优先级(越小越高)	运算符	说明	结合性
1	()	聚组:a*(b+c)	N/A
2	[] () . ++ --	数组下标[],方法参数fun(arg1,arg2,arg3),属性访问a.b,自增/减后缀a++ a--	L - R
3	++ -- + - !	自增/减前缀++a --a,正负号(一般正号不写)a ,-a,取反!false	R - L
4	* /	乘除数学运算	L - R
5	+ -	加减数学运算	L - R
7	< > <= >=	关系运算符	L - R
8	== !=	相等性运算符	L - R
12	&&	逻辑与	L - R
13	^^	逻辑排他或(用处基本等于!=)	L - R
14	||	逻辑或	L - R
15	? :	三目运算符	L - R
16	= += -= *= /=	赋值与复合赋值	L - R
17	,	顺序分配运算	L - R

关于 左值与右值：

左值:表示一个储存位置,可以是变量,也可以是表达式,但表达式最后的结果必须是一个储存位置.

右值:表示一个值, 可以是一个变量或者表达式再或者纯粹的值.

操作符的优先级：决定含有多个操作符的表达式的求值顺序，每个操作的优先级不同.

操作符的结合性：决定相同优先级的操作符是从左到右计算，还是从右到左计算。

各类型变量在计算中可能遇到如下的情况：

1.同类型 float int 间运算：

float与float , int与int之间可以直接运算。

2.不同类型 float int 间运算:

float 与 int 之间进行运算，需要进行一次显示转换.即要么把float转成int: int(1.0) ,要么把int转成float: float(1) ,以下表达式都是正确的:

```
int a=int(2.0);
float a= float(2);

int a=int(2.0)*2 + 1;
float a= float(2)*6.0+2.3;
```

3.float 与 vec(向量) mat(矩阵) 运算:

vec,mat这些类型其实是由float复合而成的,当它们与float运算时,其实就是在每一个分量上分别与float进行运算,这就是所谓的逐分量运算.glsl里 大部分涉及vec,mat的运算都是逐分量运算,但也并不全是. 下文中就会讲到特例.

逐分量运算是线性的,这就是说 vec 与 float 的运算结果是还是 vec.

int 与 vec,mat之间是不可运算的, 因为vec和mat中的每一个分量都是 float 类型的. 无法与int进行逐分量计算.

下面枚举了几种 float 与 vec,mat 运算的情况:

```
vec3 a = vec3(1.0, 2.0, 3.0);
mat3 m = mat3(1.0);
float s = 10.0;
vec3 b = s * a; // vec3(10.0, 20.0, 30.0)
vec3 c = a * s; // vec3(10.0, 20.0, 30.0)
mat3 m2 = s * m; // = mat3(10.0)
mat3 m3 = m * s; // = mat3(10.0)
```

4.vec(向量) 与 vec(向量):

两向量间的运算首先要保证操作数的阶数都相同.否则不能计算.例如: vec3*vec2 vec4+vec3 等等都是不行的.

它们的计算方式是两操作数在同位置上的分量分别进行运算,其本质还是逐分量进行的,这和上面所说的float类型的 逐分量运算可能有一点点差异,相同的是 vec 与 vec 运算结果还是 vec, 且阶数不变.

```

vec3 a = vec3(1.0, 2.0, 3.0);
vec3 b = vec3(0.1, 0.2, 0.3);
vec3 c = a + b; // = vec3(1.1, 2.2, 3.3);
vec3 d = a * b; // = vec3(0.1, 0.4, 0.9);

```

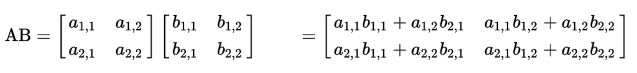
5.vec(向量) 与 mat(矩阵):

要保证操作数的阶数相同,且vec与mat间只存在乘法运算.

它们的计算方式和线性代数中的矩阵乘法相同,不是逐分量运算.

```
vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2.,  3., 4.);
vec2 w = m * v; // = vec2(1. * 10. + 3. * 20., 2. * 10. + 4. * 20.)
...

vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2.,  3., 4.);
vec2 w = v * m; // = vec2(1. * 10. + 2. * 20., 3. * 10. + 4. * 20.)
```
向量与矩阵的乘法规则如下:

![](img/2018-11-06-shader-lession-2/v-m1.png)

![](img/2018-11-06-shader-lession-2/v-m2.png)

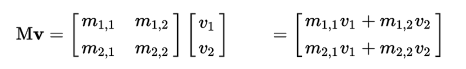
6.mat(矩阵) 与 mat(矩阵):

要保证操作数的阶数相同.

在mat与mat的运算中, 除了乘法是线性代数中的矩阵乘法外.其余的运算任为逐分量运算.简单说就是只有乘法是特殊的,其余都和vec与vec运算类似.

```
mat2 a = mat2(1., 2.,  3., 4.);
mat2 b = mat2(10., 20.,  30., 40.);
mat2 c = a * b; //mat2(1.*10.+3.*20.,2.*10.+4.*20.,1.* 30.+3.*40.,2.* 30.+4.*40.);

mat2 d = a+b;//mat2(1.+10.,2.+20.,3.+30.,4.+40);
```
矩阵乘法规则如下:

![](img/2018-11-06-shader-lession-2/m-m.png)

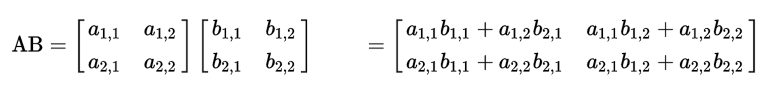类型转换

GLSL 可以通过构造函数进行显式转换，方法如下：

bool t= true;
bool f = false;

int a = int(t); //true转换为1或1.0
int a1 = int(f);//false转换为0或0.0

float b = float(t);
float b1 = float(f);

bool c = bool(0);//0或0.0转换为false
bool c1 = bool(1);//非0转换为true

bool d = bool(0.0);
bool d1 = bool(1.0);

精度限定

glsl在进行光栅化着色的时候,会产生大量的浮点数运算,这些运算可能是当前设备所不能承受的,所以glsl提供了3种浮点数精度,我们可以根据不同的设备来使用合适的精度.

在变量前面加上 highp mediump lowp 即可完成对该变量的精度声明.

lowp float color;
varying mediump vec2 Coord;
lowp ivec2 foo(lowp mat3);
highp mat4 m;

我们一般在片元着色器(fragment shader)最开始的地方加上 precision mediump float; 便设定了默认的精度.这样所有没有显式表明精度的变量 都会按照设定好的默认精度来处理.

如何确定精度:

变量的精度首先是由精度限定符决定的,如果没有精度限定符,则要寻找其右侧表达式中,已经确定精度的变量,一旦找到,那么整个表达式都将在该精度下运行.如果找到多个, 则选择精度较高的那种,如果一个都找不到,则使用默认或更大的精度类型.

uniform highp float h1;
highp float h2 = 2.3 * 4.7; //运算过程和结果都 是高精度
mediump float m;
m = 3.7 * h1 * h2; //运算过程 是高精度
h2 = m * h1; //运算过程 是高精度
m = h2 – h1; //运算过程 是高精度
h2 = m + m; //运算过程和结果都 是中等精度
void f(highp float p); // 形参 p 是高精度
f(3.3); //传入的 3.3是高精度

invariant关键字:

由于shader在编译时会进行一些内部优化,可能会导致同样的运算在不同shader里结果不一定精确相等.这会引起一些问题,尤其是vertx shader向fragmeng shader传值的时候. 所以我们需要使用invariant 关键字来显式要求计算结果必须精确一致. 当然我们也可使用 #pragma STDGL invariant(all)来命令所有输出变量必须精确一致, 但这样会限制编译器优化程度,降低性能.

#pragma STDGL invariant(all) //所有输出变量为 invariant
invariant varying texCoord; //varying在传递数据的时候声明为invariant

限定符的顺序:

当需要用到多个限定符的时候要遵循以下顺序:

1.在一般变量中: invariant > storage > precision

2.在参数中: storage > parameter > precision

我们来举例说明:

invariant varying lowp float color; // invariant > storage > precision

void doubleSize(const in lowp float s){ //storage > parameter > precision
    float s1=s;
}

内置函数库

glsl提供了非常丰富的函数库,供我们使用,这些功能都是非常有用且会经常用到的. 这些函数按功能区分大改可以分成7类:

通用函数:

下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T abs(T x)	返回x的绝对值
T sign(T x)	比较x与0的值,大于,等于,小于 分别返回 1.0 ,0.0,-1.0
T floor(T x)	返回<=x的最大整数
T ceil(T x)	返回>=等于x的最小整数
T fract(T x)	获取x的小数部分
T mod(T x, T y) T mod(T x, float y)	取x,y的余数
T min(T x, T y) T min(T x, float y)	取x,y的最小值
T max(T x, T y) T max(T x, float y)	取x,y的最大值
T clamp(T x, T minVal, T maxVal) T clamp(T x, float minVal,float maxVal)	min(max(x, minVal), maxVal),返回值被限定在 minVal,maxVal之间
T mix(T x, T y, T a) T mix(T x, T y, float a)	取x,y的线性混合,x(1-a)+y\a
T step(T edge, T x) T step(float edge, T x)	如果 x<edge 返回 0.0 否则返回1.0
T smoothstep(T edge0, T edge1, T x) T smoothstep(float edge0,float edge1, T x)	如果x<edge0 返回 0.0 如果x>edge1返回1.0, 否则返回Hermite插值

角度&三角函数:

下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T radians(T degrees)	角度转弧度
T degrees(T radians)	弧度转角度
T sin(T angle)	正弦函数,角度是弧度
T cos(T angle)	余弦函数,角度是弧度
T tan(T angle)	正切函数,角度是弧度
T asin(T x)	反正弦函数,返回值是弧度
T acos(T x)	反余弦函数,返回值是弧度
T atan(T y, T x) T atan(T y_over_x)	反正切函数,返回值是弧度

指数函数:

下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
T pow(T x, T y)	返回x的y次幂 xy
T exp(T x)	返回x的自然指数幂 ex
T log(T x)	返回x的自然对数 ln
T exp2(T x)	返回2的x次幂 2x
T log2(T x)	返回2为底的对数 log2
T sqrt(T x)	开根号 √x
T inversesqrt(T x)	先开根号,在取倒数,就是 1/√x

几何函数:

下文中的 类型 T可以是 float, vec2, vec3, vec4,且可以逐分量操作.

方法	说明
float length(T x)	返回矢量x的长度
float distance(T p0, T p1)	返回p0 p1两点的距离
float dot(T x, T y)	返回x y的点积
vec3 cross(vec3 x, vec3 y)	返回x y的叉积
T normalize(T x)	对x进行归一化,保持向量方向不变但长度变为1
T faceforward(T N, T I, T Nref)	根据 矢量 N 与Nref 调整法向量
T reflect(T I, T N)	返回 I - 2 dot(N,I) N, 结果是入射矢量 I 关于法向量N的 镜面反射矢量
T refract(T I, T N, float eta)	返回入射矢量I关于法向量N的折射矢量,折射率为eta

矩阵函数:

mat可以为任意类型矩阵.

方法	说明
mat matrixCompMult(mat x, mat y)	将矩阵 x 和 y的元素逐分量相乘

向量函数:

下文中的 类型 T可以是 vec2, vec3, vec4, 且可以逐分量操作.

bvec指的是由bool类型组成的一个向量:

vec3 v3= vec3(0.,0.,0.);
vec3 v3_1= vec3(1.,1.,1.);
bvec3 aa= lessThan(v3,v3_1); //bvec3(true,true,true)

方法	说明
bvec lessThan(T x, T y)	逐分量比较x < y,将结果写入bvec对应位置
bvec lessThanEqual(T x, T y)	逐分量比较 x <= y,将结果写入bvec对应位置
bvec greaterThan(T x, T y)	逐分量比较 x > y,将结果写入bvec对应位置
bvec greaterThanEqual(T x, T y)	逐分量比较 x >= y,将结果写入bvec对应位置
bvec equal(T x, T y) bvec equal(bvec x, bvec y)	逐分量比较 x == y,将结果写入bvec对应位置
bvec notEqual(T x, T y) bvec notEqual(bvec x, bvec y)	逐分量比较 x!= y,将结果写入bvec对应位置
bool any(bvec x)	如果x的任意一个分量是true,则结果为true
bool all(bvec x)	如果x的所有分量是true,则结果为true
bvec not(bvec x)	bool矢量的逐分量取反

纹理查询函数:

图像纹理有两种 一种是平面2d纹理,另一种是盒纹理,针对不同的纹理类型有不同访问方法.

纹理查询的最终目的是从sampler中提取指定坐标的颜色信息. 函数中带有Cube字样的是指 需要传入盒状纹理. 带有Proj字样的是指带投影的版本.

以下函数只在vertex shader中可用:

vec4 texture2DLod(sampler2D sampler, vec2 coord, float lod);
vec4 texture2DProjLod(sampler2D sampler, vec3 coord, float lod);
vec4 texture2DProjLod(sampler2D sampler, vec4 coord, float lod);
vec4 textureCubeLod(samplerCube sampler, vec3 coord, float lod);

以下函数只在fragment shader中可用:

vec4 texture2D(sampler2D sampler, vec2 coord, float bias);
vec4 texture2DProj(sampler2D sampler, vec3 coord, float bias);
vec4 texture2DProj(sampler2D sampler, vec4 coord, float bias);
vec4 textureCube(samplerCube sampler, vec3 coord, float bias);

在 vertex shader 与 fragment shader 中都可用:

vec4 texture2D(sampler2D sampler, vec2 coord);
vec4 texture2DProj(sampler2D sampler, vec3 coord);
vec4 texture2DProj(sampler2D sampler, vec4 coord);
vec4 textureCube(samplerCube sampler, vec3 coord);

到现在，所有 GLSL 的基本知识都已经介绍完毕了，下一节我们开始尝试自己写一些 shader。