工作后基本就再没机会再使用这些知识了,有点小怀念的说。本期给他拉到一起,做一个特辑。
既然一连串写了这么多马。

如果您没见过这些马,我想内心一定会很崩溃, 来来~ uncle.wang 带你逐个击破:
真值
真值是最容易理解的,他指的是数学上的数字,是有正负的。其他各种码都是在此基础上进行的演化。一般来说,真值指是十进制数,而在计算机中使用的是二进制,下面来看一下二进制的转换方法:
十进制转二进制,最常用的短除法:
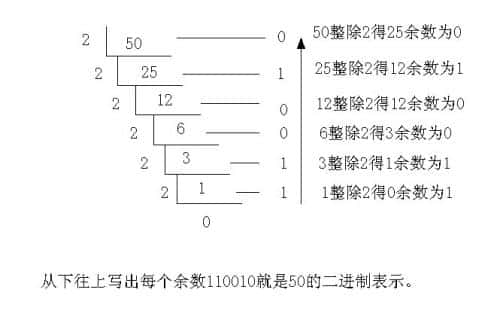
二进制转十进制,常用展开法:
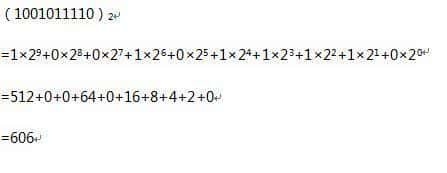
javascript 中使用 number 的 toString(radix) 即可完成转换:
const num = 168;
num.toString(2); //转换换成 2 进制
num.toString(8); //转换换成 8 进制
num.toString(16); //转换换成 8 进制
... ...
parseInt("6f",16); //转换 16进制到 10 进制
... ...机器数
机器数是真值在机器中的表示,是二进制的。机器数受硬件限制,所以机器数只能尽可能的接近真值。
在机器数中对符号有特殊的规定,起始位 0 代表正数,1 代表负数。根据表示方法不同,机器数分为:原码、反码、补码、移码等。
在计算机中,所有数字都是以补码的形式储存的。
原码
原码很简单,就是最高位作为符号位,其余位表示真值的绝对值。
比如在一个 8 位计算机中:
[+1] 原 = 0000 0001
[-1] 原 = 1000 0001反码
正数的 反码 就是 其 原码本身 ,负数 的反码则是 符号位不变 ,其余位取反。
反码的运算方法为 循环进位,即 最高位的进位要加到最低位来。如:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补产生的原因:
可见原码, 反码和补码是完全不同的,那这样做有何意义呢?
计算机的所有计算本质上都是加法,然而若正负值相加时让计算机判断符号位来选择运算方式会使得加法电路设计变得复杂,但是若直接让符号位参与运算则会带来 1 + (-1) = -2 (8位为例:00000001 + 10000001 = 10000010) 这类的问题,使用反码就是为了解决 符号位参与运算 的加法问题。
用反码计算减法, 结果的真值部分是正确的, 减一个数就等于加它的反码,但是问题在于他会出现两个 0 值,即 正 0 和 负 0 ,虽然在人们理解上 +0 和 -0 是一样的, 但是 0 带符号是没有任何意义的。
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
+0 = 0000 0000
-0 = 1111 1111补码
反码是一个不完美的解决方案,有不近人意的问题。比如: 8位为例,0000 0000 和 1111 1111 都可以表示零,一个 +0,一个 -0。为了解决这个问题,引入补码来表示数值。
正数 的补码是 其原码本身 ,负数 的补码是 其反码 + 1 。这个设计使得加法运算满足一个等式:a(补) + b(补) = (a + b)(补) ,由此,不管符号为何,直接参与运算都能得到正确的结果。目前补码是最佳的解决方案。 现行的编程语言,都是用补码来表示数值和进。
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为 [-128, 127].
补码的原理用一个例子来解释:
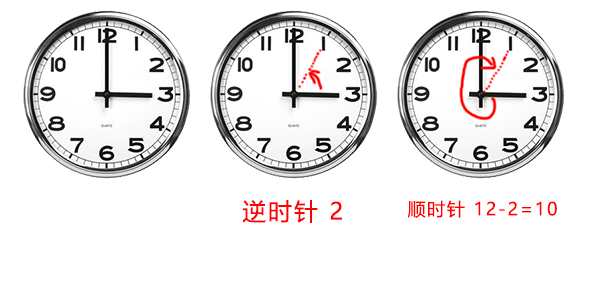
这是一个钟表,3 点钟。现要想减少 2 小时,怎么办呢?
第一个办法:逆时针拨动 2 个小时。
第二个办法:顺时针拨动 10 个(12-2) 小时
都可以得到同样的效果。
对于时钟来讲 12 是他的模,但对于二进制数来说 2^n+1 是模。也就是说假设要对 -3 (111,符号 值)这个机器数求补,则结果为 模 - 绝对值 1000 - 011 = 1 001
移码
移码则是 把补码的符号位取反,常常用在 浮点 数值的二进制表示中。
浮点数的二进制表示比较特殊,整个二进制位分为三个部分:
| 类型 | 符号位 | 阶码 | 尾数 | 总位数 |
|---|---|---|---|---|
| float | 1 | 8 | 23 | 32 |
| double | 1 | 11 | 52 | 64 |

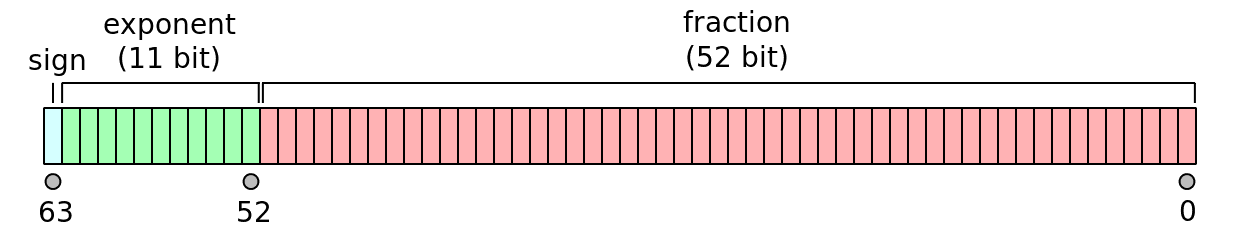
设阶码为 e,尾数为 m,则浮点的值为: m∗(2^e),其中阶码是用移码表示。
用移码表示的原因在于,阶码作为指数是有正负的,用移码表示能在 不考虑阶码符号 的情况下比较浮点数大小。如:(8位情况下) 11111111 是最小值,00000000 是 0 如果不考虑符号,则 11111111 > 00000000 显然不方便。而用移码则:11111111 -> 00000001,00000000 -> 10000000 大小一下就比较出来了。
阶码确定浮点数的取值范围,尾数确定浮点数的精度。
BCD码
BCD 码又称 (Binary-Coded Decimal),用 4 位二进制数来表示 1 位十进制数中的 0~9 这 10 个数码。是一种二进制的数字编码形式。BCD 码可分为有权码和无权码两类:有权 BCD 码有 8421 码、2421 码、5421 码,其中 8421 码是最常用的;无权 BCD 码有 余 3 码,余 3 循环码等。
| 十进制数 | 8421 码 | 5421 码 | 2421 码 | 余 3 码 | 余 3 循环码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 | 0010 |
| 1 | 0001 | 0001 | 0001 | 0100 | 0110 |
| 2 | 0010 | 0010 | 0010 | 0101 | 0111 |
| 3 | 0011 | 0011 | 0011 | 0110 | 0101 |
| 4 | 0100 | 0100 | 0100 | 0111 | 0100 |
| 5 | 0101 | 1000 | 1011 | 1000 | 1100 |
| 6 | 0110 | 1001 | 1100 | 1001 | 1101 |
| 7 | 0111 | 1010 | 1101 | 1010 | 1111 |
| 8 | 1000 | 1011 | 1110 | 1011 | 1110 |
| 9 | 1001 | 1100 | 1111 | 1100 | 1010 |
余三码
余三码就是给 8421 码加上 0011 即 加 +3 后的码,为什么要这么做呢?
原因是 BCD 码虽然方便,但是有个问题,即: 4 位二进制可以表示 16 个数,但十进制一共仅有 0-9 十个位置,剩下 6 个怎么办? 尤其是在相加产生进位的时候,这个问题非常凸显。
比如下面:
7 + 8 = 15
则 0111 + 1000 = 1111 但是你会发现 8421 码中根本没有 1111 。这怎么办?
余三码是一种对 9 的自补代码,因而可给运算带来方便。其次,在将两个余三码表示的十进制数相加时,能正确产生进位信号,但对“和”必须修正。修正的方法是:如果有进位,则结果加3;如果无进位,则结果减 3。
加 3 转换成 余三码 后我们来看:
7 + 8 = 15 -> 10 + 11 = 21 -> 21 - 16 = 5
1010 + 1011 = 0001 0101 产生进位了所以 0101 + 0011 = 1000
1 + 2 = 3 -> 4 + 5 = 9
0100 + 0101 = 1001 没有产生进位了所以 1001 - 0011 = 0110
计算的关键在于 余三码 相加后结果一定要保证还是 余三码。
格雷码 (Gray Code)
格雷码在数控电路中经常用到,它的最基本意义是: 任意两个相邻的代码只有一位二进制数不同。 这样可以避免数字变化引起的抖动。举个例子来说:
5 的二进制: 0101
6 的二进制: 0110
那么设想有一部电梯,电梯中有个显示楼层的 LCD 屏幕,从 5 层切换到 6 层,则在二进制层面为: 0101 + 0001 = 0110 ,但在实际电路中,因为这一步骤涉及两个数位变换,完成需要分两步进行:

上图中 0101 先变成 0111 再变成 0110,不管先变化哪一位? 这中间的产物 0111 (或者 0100) 都将成为干扰。
为了避免这种情况,我们需要相邻两个数之间只能有 1 位数位的变化。这既是 格雷码 (Gray Code)
- 二进制码转换成二进制格雷码:
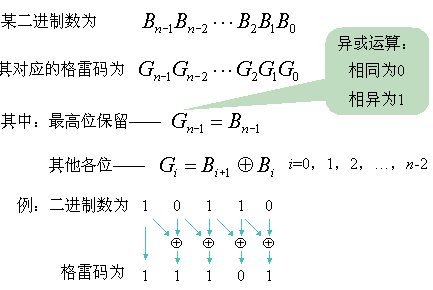
总结:格雷码的值只需要在原来的二进制的基础上右移一位再加上原来的二进制值即可得到。
- 二进制格雷码转换成二进制码
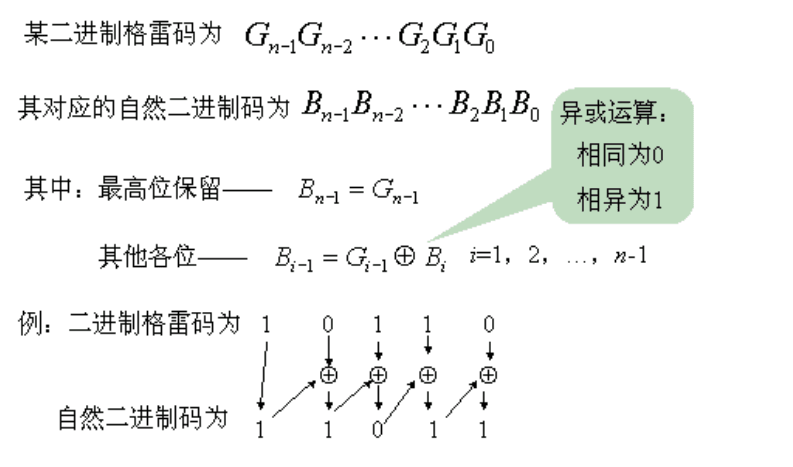
余三循环码
余三循环可以理解为是满足格雷码特性的余三码,直接计算 余三码的格雷码即可。
奇偶校验码
无论数据位多少位,校验位只有一位
数据位和校验位 一共 所含的1个数为奇数,称为奇校验
数据位和校验位 一共 所含的1个数为偶数,称为偶校验
| 数据 | 奇校验的编码 | 偶校验的编码 |
|---|---|---|
| 00000000 | 100000000 | 000000000 |
| 01010100 | 001010100 | 101010100 |
| 01111111 | 001111111 | 101111111 |
实现原理:那么,奇偶校验是怎么来发现错误的呢?根据数据是如何校验的我们可以知道,在数据传输之前,我们会求一次校验位,传输后,会求一次校验位,那么,在奇偶校验中,我们通过比较这两个校验位是否相同,一般是采用异或的方式,若结果为1,则说明有奇数个错误,结果为0,则说明正确或者偶数个错误。
CRC码
详细参见: https://www.cnblogs.com/sinferwu/p/7904279.html
CRC即循环冗余校验码:是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的 结果附在帧的后面 ,接收设备也执行类似的算法,以保证数据传输的正确性和完整性
为什么大批量数据不用奇偶校验?
因为在每个字符后增加一位校验位会增加大量的额外开销;尤其在网络通信中,对传输的二进制比特流没有必要再分解成一个个字符,因而无法采用奇偶校验码。
CRC 算法的基本思想是将传输的数据当做一个位数很长的数。将这个数除以另一个数。得到的余数作为校验数据附加到原数据后面。但这个除数选取很有讲究,好在已经有无数专家帮我们研究过了,CRC 常用除数(多项式的系数)如下:
| 名称 | 生成多项式 | 简记式 | 标准引用 |
|---|---|---|---|
| CRC-4 | x4+x+1 | 3 | ITU G.704 |
| CRC-8 | x8+x5+x4+1 | 0x31 | |
| CRC-8 | x8+x2+x1+1 | 0x07 | |
| CRC-8 | x8+x6+x4+x3+x2+x1 | 0x5E | |
| CRC-12 | x12+x11+x3+x+1 | 80F | |
| CRC-16 | x16+x15+x2+1 | 8005 | IBM SDLC |
| CRC16-CCITT | x16+x12+x5+1 | 1021 | ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCS |
| CRC-32 | x32+x26+x23+...+x2+x+1 | 04C11DB7 | ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCS |
| CRC-32c | x32+x28+x27+...+x8+x6+1 | 1EDC6F41 | SCTP |
有一点要特别注意,文献中提到的生成多项式经常会说到多项式的位宽(Width,简记为W),这个位宽不是多项式对应的二进制数的位数,而是位数减1。比如CRC8中用到的位宽为8的生成多项式,其实对应得二进制数有九位:100110001。另外一点,多项式表示和二进制表示都很繁琐,交流起来不方便,因此,文献中多用16进制简写法来表示,因为生成多项式的最高位肯定为1,最高位的位置由位宽可知,故在简记式中,将最高的1统一去掉了,如CRC32的生成多项式简记为 04C11DB7 实际上表示的是 104C11DB7。当然,这样简记除了方便外,在编程计算时也有它的用处。
CRC 的计算过程:
下图 CRC生成多项式为G(X) = X4 + X3 + 1,要求出二进制序列 10110011 的 CRC 校验码。
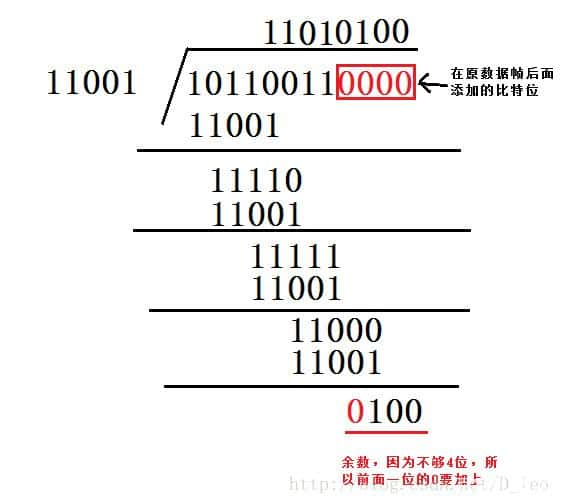
下面是具体的计算过程:
①将多项式转化为二进制序列,由G(X) = X4 + X3 + 1可知二进制一种有五位,第4位、第三位和第零位分别为 1,则序列为 11001
②多项式的位数位5,则在数据帧的后面加上 5-1 位 0,数据帧变为 101100110000,然后使用模 2 除法除以除数 11001,得到余数。
③将计算出来的CRC校验码添加在原始帧的后面,真正的数据帧为 101100110100,再把这个数据帧发送到接收端。
④接收端收到数据帧后,用上面选定的除数,用模 2 除法除去,验证余数是否为0,如果为0,则说明数据帧没有出错。